

optweight contains functions to estimate stable balancing
weights that balance covariates up to given thresholds. It solves a
convex optimization problem to minimize a function of the weights that
captures their variability (or divergence from a set of base weights).
This is the method described in Zubizarreta (2015), Källberg and
Waernbaum (2023),
and Wang and Zubizarreta (2020).
optweight extends the method to multi-category, continuous, and
multivariate treatments and provides a simple user interface and
compatibility with the cobalt package for balance assessment.
See vignette("optweight") for a more thorough description
of the package’s capabilities.
To install optweight, use the code below:
#CRAN version
install.packages("optweight")
#Development version
pak::pkg_install("ngreifer/optweight")Below is an example of estimating weights with optweight and assessing balance on the covariates with cobalt.
library("optweight")
library("cobalt")
data("lalonde")
# Estimate weights
ow <- optweight(treat ~ age + educ + race + nodegree + married +
re74 + re75,
data = lalonde,
estimand = "ATT",
tols = .01,
min.w = 0)
ow#> An optweight object
#> - number of obs.: 614
#> - norm minimized: "l2"
#> - sampling weights: present
#> - base weights: present
#> - treatment: 2-category
#> - estimand: ATT (focal: 1)
#> - covariates: age, educ, race, nodegree, married, re74, re75# Information about the weights
summary(ow)#> Summary of weights:
#>
#> - Weight ranges:
#> Min Max
#> treated 1 || 1.
#> control 0 |---------------------------| 5.5885
#>
#> - Units with 5 greatest weights by group:
#>
#> 1 2 3 4 5
#> treated 1 1 1 1 1
#> 423 388 226 196 118
#> control 5.2698 5.2985 5.3241 5.4795 5.5885
#>
#> L2 L1 L∞ # Zeros
#> treated 0. 0. 0. 0
#> control 1.663 1.302 4.588 231
#>
#> - Effective Sample Sizes:
#> Control Treated
#> Unweighted 429. 185
#> Weighted 113.9 185# Covariate balance
bal.tab(ow)#> Balance Measures
#> Type Diff.Adj
#> age Contin. 0.01
#> educ Contin. 0.01
#> race_black Binary 0.01
#> race_hispan Binary 0.00
#> race_white Binary -0.01
#> nodegree Binary 0.01
#> married Binary -0.01
#> re74 Contin. -0.01
#> re75 Contin. 0.01
#>
#> Effective sample sizes
#> Control Treated
#> Unadjusted 429. 185
#> Adjusted 113.9 185We can see that all standardized mean differences are at or below .01
in absolute value, as requested using the tols argument.
Because we set min.w = 0, some units received weights of 0,
effectively dropping them from the sample (by default, the smallest
weight allowed is \(10^{-8}\)).
We can use plot() to examine the dual variables for each
constraint, which represent how active that constraint is at the optimal
point. Highly active constraints affect the objective function value the
most when their tolerances are changed.
plot(ow)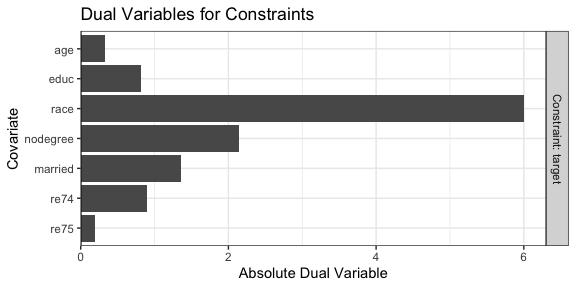
We can see that race has the highest dual variable;
relaxing the constraint on race would yield the biggest
improvement in effective sample size, while tightening its constraint
would yield the biggest decrease in effective sample size.
The lower-level function optweight.fit() operates on the
covariates and treatment variables directly. optweightMV()
supports multivariate (i.e., multiple) treatments.
In addition to estimating balancing weights for estimating treatment
effects, optweight can estimate sampling weights for
generalizing an estimate to a new target population defined by covariate
moments using optweight.svy().
To cite optweight, please use
citation("optweight") to generate the correct reference. Be
sure to include the version of the package. Please submit bug reports,
questions, comments, or other issues to https://github.com/ngreifer/optweight/issues.